|
دوستداران ریاضی در ریاضیات، مربع کامل عددی صحیح است که به صورت مجذور یک عدد صحیح دیگر باشد، یا به عبارتی بتوان آن را به صورت ضرب یک عدد طبیعی در خودش نوشت. مثلاً عدد ۲۵ یک مربع کامل است چون میتوان آن را به صورت ۵×۵ نوشت. مربع کامل غیر منفی است و روش دیگر تعریف آن این است که بگوییم ریشه دوم آن عددی صحیح باشد، مثلاً اگر مربع عدد زوج و یا مربع عدد فرد را بر 4 تقسیم کنیم باقیمنده 0 یا 1 می شود. هر عددی که مربع کامل باشد. رقم دهگانش زوج است. معادلات درجه دو با روشهای فاکتورگیری، مربع کامل کردن، نمودار تابع(رسم نمودار)، روش نیوتون و روشهای دیگر حل میشوند. فاکتورگیریاین روش موقعی کارایی مناسبی دارد که بتوان به طریقی با تقسیم کل معادله بر ضریب جمله به سرعت به ذهنمان برسد. به این روش که منتج شده از اتّحاد ریاضیاتی معروف به جمله مشترک است ، روش حل تجزیهای هم گفته میشود. سپس معادله بر اساس این اتحاد به شکل مثال: میخواهیــم معادله روش مربـّـع کامل کردن این روش بر مبنای یکی از معروفترین اتّحادهای ریاضی ، معروف به اتحاد مربـّـع دوجملهای به دست آمدهاست. برای هر دو عبارت ریاضی مثل A و B این اتحاد به این صورت ارائه میگردد: حال ما باید
مثال : میخواهیم دستگاه مختصات دکارتی، در هندسه، به نمایش هر نقطه از صفحه با دو عدد (یک زوج مرتب) گفته میشود. این دو عدد را معمولاً به نامهای مختصه X و مختصه Y میخوانند. در دستگاه محورهای مختصات دوبعدی، محورهای X و Y بر هم عمودند، از همین رو این دستگاه را دستگاه محورهای متعامد نیز میگویند. برای نمایش هندسی هر نقطه، دو خط عمود بر هم را، که محور مختصات X (خِفت یا آبسیس) و محور مختصات Y، (یا اردنه) نامیده میشوند، رسم میکنند و از محل تقاطع این دو محور، که مبدا مختصات نام دارد، روی هر محور به اندازه مختصه X و مختصه Y دو طول را (بر حسب واحد طول) مشخص میکنند. خطهایی که در انتهای این طولها عمود بر محورهای مختصات رسم شود در نقطهای یکدیگر را قطع میکنند. این محل تقاطع نمایش هندسی نقطه مورد نظر است. نام این دستگاه مختصات از نام ریاضیدان و فیلسوف فرانسوی رنه دکارت (۱۵۹۶-۱۶۵۰) که این روش را برای مشخص کردن یک نقطه در صفحه کشف کرد، گرفته شدهاست. با کاربرد دستگاه مختصات دکارتی امکان رسم معادلات جبری به صورت خط و منحنی و یا محاسبه زوایا و فواصل و همچنین نوشتن معادله مختصات یک شکل در صفحه فراهم میشود.
فرمول های مهم مثلثات برای تبدیل و محاسبه
  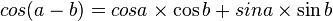    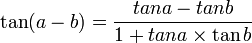  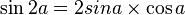 ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ (فرمول طلایی)   ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ (تبدیل ضرب به جمع)    ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ (تبدیل جمع به ضرب)  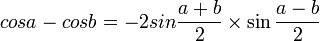   ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ نسبت های مثلثاتی بر حسب   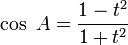  ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــــــ ـــــــــــــــــــــ فرمول کاشانی که در هر مثلثی صدق میکند 
در مثلث قائمالزاویه نسبت ضلع مجاور هر زاویه حاده به وتر را کسینوس آن زاویه مینامند. جبر خطّی شاخهای از ریاضیات است که به بررسی و مطالعۀ ماتریسها، بردارها، فضاهای برداری (فضاهای خطّی)، تبدیلات خطی، و دستگاههای معادلات خطی میپردازد. جبر خطّی و کارائیهای فراوان و گوناگون آن در ریاضیات و محاسبات گسسته طیف گسترده و وسیعی را شامل میگردد. علاوه بر کاربردهای آن در زمینههایی از خود ریاضیات همانند جبر مجرد، آنالیز تابعی، هندسۀ تحلیلی، و آنالیز عددی، جبر خطّی استفادههای وسیعی نیز در فیزیک، مهندسی، علوم طبیعی، و علوم اجتماعی پیداکرده است. آغاز نمودن مبحثی با اهمیت و همهجاگیری جبر خطی یکی از دشوارترین کارهاست، چرا که، با جهتگیریها، تعبیرات، تعمیمات، و آیندهبینیهای زیادی روبرو میشویم. شاید یکی از انتخابهای مناسب این گونه باشد: ماتریس و بردار زیر را در نظر میگیریم:
با ضرب ماتریس و بردار داریم:
نتیجهٔ فوق را میتوان در ترازهای معنائی گوناگونی مورد دقت و بررسی قرار داد. برخی از ملاحظات این گونه است: ماتریس سیستم
است.
مثلث خیام را در برخی منابع به ندرت «مثلث خیام-پاسکال-نیوتن» نیز میگویند. این مثلث در زبانهای گوناگون نامهای دیگری نیز دارد در زبان انگلیسی «مثلث پاسکال»، ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفتهاست. در آثار متون سانسکریتِ پینگالا ریاضیدان هندی نشانههایی از استفاده از این بسط دیده میشود. در همان دوران عمر خیام ریاضیدان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجملهای میکند. کتاب «مشکلات الحساب»، کتابی که اثباتهای این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تأثیر گرفته از او ضرایب را تا توان ۱۲ میتوان دید[۲]. بعد از او در قرن ۱۲ میلادی در آثار یانگ هویی ریاضیدان چینی، شکل مثلث به چشم میخورد. در قرن ۱۶ میلادی ریاضیدان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضیدان فرانسوی هم دوره با نیوتون روی این بسط و مثلث حسابی آن کار کرد. برای مطالعه ی خواص جمله های مثلث کافی هست از تعریف استفاده کنیم
درباره وبلاگ به وبلاگ من خوش آمدید آخرین مطالب آرشيو وبلاگ نويسندگان پيوندها
|
|||
|
|
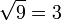 میباشد پس ۹ یک مربع کامل است. این اعداد خاصیتهای جالبی دارند از جمله اینکه تعداد مقسوم علیههای این اعداد فرد است، بنابراین یکی از راههای تشخیص این اعداد همین نکته است. نکته دیگر اینکه حاصل جمع اعداد فرد متوالی مربع کامل است یعنی: ۱=۱ ۱+۳=۴ ۱+۳+۵=۹ ۱+۳+۵+۷=۱۶ ۱+۳+۵+۷+۹=۲۵ . . . همچنین: هر عدد که ریشه ی آن ( 9*7*4*1 ) باشد. مربع کامل است.
میباشد پس ۹ یک مربع کامل است. این اعداد خاصیتهای جالبی دارند از جمله اینکه تعداد مقسوم علیههای این اعداد فرد است، بنابراین یکی از راههای تشخیص این اعداد همین نکته است. نکته دیگر اینکه حاصل جمع اعداد فرد متوالی مربع کامل است یعنی: ۱=۱ ۱+۳=۴ ۱+۳+۵=۹ ۱+۳+۵+۷=۱۶ ۱+۳+۵+۷+۹=۲۵ . . . همچنین: هر عدد که ریشه ی آن ( 9*7*4*1 ) باشد. مربع کامل است.
 دو ثابت
دو ثابت  و
و  ای به دست آورد که بین آنها رابطهای به شکل
ای به دست آورد که بین آنها رابطهای به شکل  و
و 
 در میآید و در این حالت به آسانی با برابر صفر قرار دادن هر پرانتز به جوابهای
در میآید و در این حالت به آسانی با برابر صفر قرار دادن هر پرانتز به جوابهای  میرسیم.
میرسیم. را حل کنیم. ابتدا دو طرف را بر دو تقسیم میکنیم تا ضریب
را حل کنیم. ابتدا دو طرف را بر دو تقسیم میکنیم تا ضریب 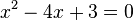 همانطور که میبینیم
همانطور که میبینیم  پس جوابها به صورت
پس جوابها به صورت  میباشند.
میباشند.
 را به صورت
را به صورت  در نظر بگیریم و
در نظر بگیریم و 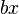 را به صورت
را به صورت  و از آنجا
و از آنجا 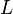 را به دست آورده و مقدار
را به دست آورده و مقدار  را از طرف چپ معادله کم و زیاد کنــیم و پس از مرتب کردن و فاکتورگیــری ، معادله را به شکل
را از طرف چپ معادله کم و زیاد کنــیم و پس از مرتب کردن و فاکتورگیــری ، معادله را به شکل درآوریم. که درصورتی معادله جواب حقیقی دارد که
درآوریم. که درصورتی معادله جواب حقیقی دارد که  مقداری مثبت یا صفر شود.
مقداری مثبت یا صفر شود. را حل کنــیم.
را حل کنــیم. 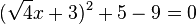 و سپس نتیجه میشود :
و سپس نتیجه میشود : 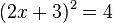 و داریــــم:
و داریــــم:  و از آنجا به دست میآوریم :
و از آنجا به دست میآوریم : 






 ). پس داریم:
). پس داریم:

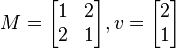

 به عنوان
به عنوان  عمل نموده و آنرا به بردار
عمل نموده و آنرا به بردار  تبدیل کرده است.
تبدیل کرده است. 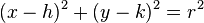
 |
| |
|

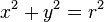
 و
و 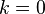 در رابطهی مرکز-شعاع دایره، به سادگی رابطهی بالا بدست میآید.
در رابطهی مرکز-شعاع دایره، به سادگی رابطهی بالا بدست میآید.
 و
و  و
و  ، شکل کلی معادله ی دایره نامیده میشود.
، شکل کلی معادله ی دایره نامیده میشود.

